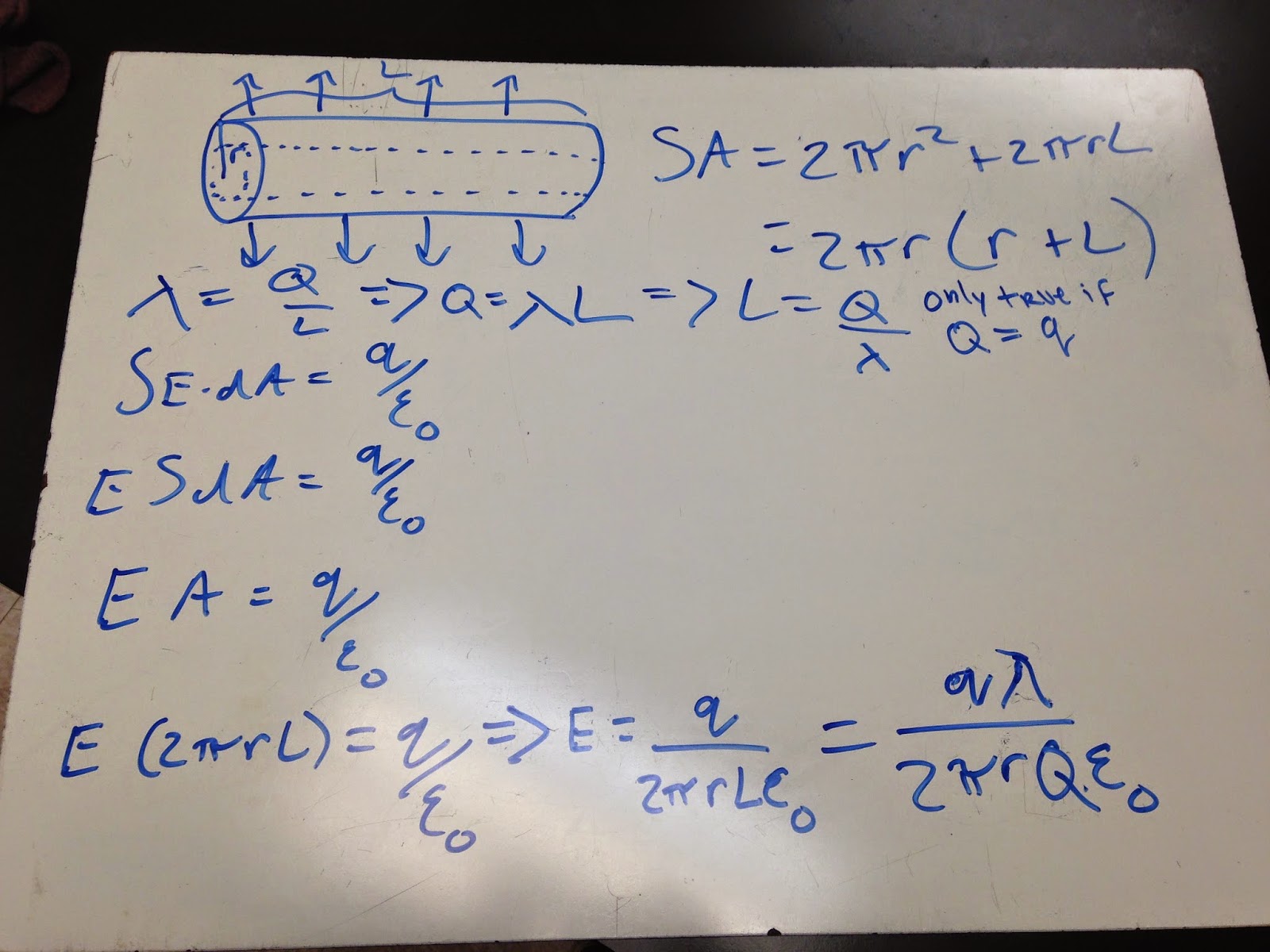Potential on a Ring around a set of charges

This here is a code for the calculation of the electric potential at various point on a ring centered around various point charges. The while reiterates as long is less than 2*pi. With each iteration, the quotient of pi/12 is added to a, allowing for a total of 24 iterations.

Each label indicates the resulting electric potential at that point due to the various charges.

Electric Potential Energy and Work

In the three previous pictures is a setup of two light bulbs connected in parallel to a power source. It is clear to see that the bulbs glow with different intensities. This indicates the power supplies to these two bulbs are different, proving that potential is not constant in across a circuit in parallel.

In an experiment where we analyzed the effects that a metal conductor connected to a source would have on the temperature of a cup of water, we see that the temperature increases steadily over time.

When the voltage is increased, the temperature rises faster.

Depicted on the left side are two lights bulbs in parallel with a power source. The lower image is the accepted representation of this setup that would be used by engineers. On the right side is the two bulbs in series connected to two batteries in parallel. The right side has a voltage equivalent to one battery. 

Doubling the voltage essentially doubles the current running through a conductor. Therefore, increasing the voltage by a factor of two, increases the current by a factor of two, which increases the power by a factor of four.

Calculating the work done to get from point a to point c, we determined that only movement parallel to the gravitational field performs work (in regards to gravity) on the object resulting in a change in gravitational potential energy. The same can be said about the change in potential energy on a charge in an electric field. Only movement parallel to the field results in change in the field. 

Depicted here is an equipotential surface. At all points on the circle, there is a constant potential. If we integrate from infinity to a distance r away from the charge, we see that the potential at r is equal to (k*Q)/r.

In the previous two pictures, we show how to calculate the potential at a point due to numerous charges. As you can see, the total potential is simply the sum the potentials due to each charge. 

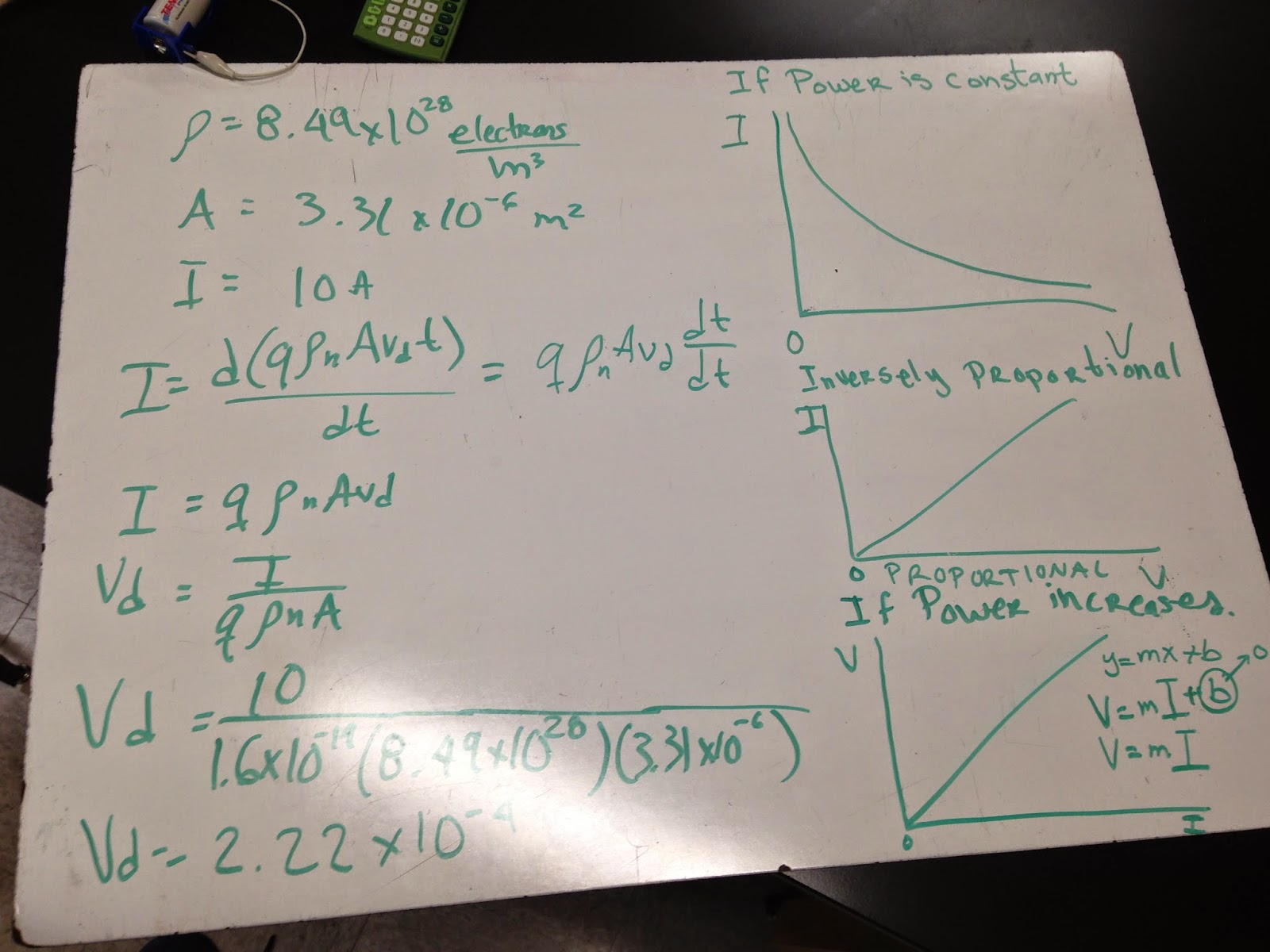
Current and Resistance

Here we are trying to light a light bulb given two batteries, a conducting wire, and the light bulb.

In order to light the light bulb, a path needs to be created that would allow charge to flow through the batteries, through the bulb, and into the wire. If the wire is connected to both terminals, then simply touching the bulb to the wire will not light the bulb since charge is not flowing through the bulb.

The device above is called an electroscope and is used to observe the presence of charge. Rubbing a metal rob with animal fur, and then placing the rod in contact with the buld will cause the filaments to repel away from each other. This is an effect of the charge that was placed on the rod due the fur traveling down into the filaments. 

If we touch the positive end of the battery to the electroscope, nothing happens because there is no path for charge to move. Also, a closed circuit is needed in order to ensure a constant flow of charge. If there were no closed circuit, then eventually, a charge would build up, and repel any incoming charges, essentially stopping the flow of charge.

In order to analyze the amount of energy flowing into and out out a bulb, we connected a multimeter in series with a light build and battery. We predicted that less energy would leave the bulb than had originally entered. However, when we connected the multimeter in series after the current passed through the bulb, we see that it is the same current that had passed into the bulb. This means the current throughout a circuit in series in constant. Knowing the drift velocity of the charge carriers, the charge of the carriers, the number of charged particles for a given volume, and the cross sectional area allows you to find the current.

When comparing the current running through a wire to the potential of one end of the wire with respect to the other end, we see that they share a linear relationship. As the current running through the wire increases, the potential (voltage) also increases.

Solving for the drift velocity, we see the it is extremely small. As electrons move through the wire, they constantly crash into other particles, slowing their progress as they make their way across the wire.

A longer wire has more resistance than a shorter wire of the same material since their is more material. We see that the ratios of the resistances are the same as their ratio of their lengths. We can use this ratio to solve for unknown ratios and unknown lengths. Also, increasing the diameter of a wire creates less resistance. This is analogous to a water hose with a wide opening being able to push more water through relative a a water hose of smaller diameter.

Gauss' Law

Enclosing the earth in a sphere of a radius equal to the radius of the earth plus the height from the surface, we can solve for gravitational acceleration. *Note - our value for G should actually be 6.67*10^-11. 

A cylindrical gaussian surface located inside a long conducting wire shares the same linear charge density as the wire. We therefore can create a relationship between the charge q inside the smaller cylinder of radius r and the charge Q inside the wire of radius R. Solving for the flux through the gaussian surface, we can replace q with the relationship formed between the two charges.

Inducing a charge on the surface of a conducting cylinder will cause any excess of charge to lie on the surface. Therefore, if we were to place pieces of foil paper on the cylinder, they would eventually experience a charge as well. As this occurs, the charge on the foil paper repels away from the charge on the cylinder.

This Van de Graff  electrostatic generator is what was used to induce the charge on the cylinder.

A sphere of radius r inside a larger sphere of radius r shares the same charge density (Q/V). This allows us to create a relationship between the charge inside both spheres and the radius of the spheres (Q/R^3 = q/r^3). Since the flux through the sphere smaller radius is E dot 4*pi*r^2, and the charge enclosed by that sphere is Q*r^3/R^3, we see that we can solve for the electric field caused the charge enclosed in the smaller sphere. Also, we can see that if the radius of the "Smaller" sphere is the same as that of the larger sphere, the electric field reduces to that kq/r^2, the same as the electric field of a point charge at a distance r away.

The smaller cylinder inside the larger cylinder shares the same charge density as the larger cylinder. This allows us to create a relationship between the charge inside the cylinders, and the radius of the cylinders. If the radius of the smaller cylinder is only half that of the larger one, than the charge enclosed by that cylinder is only one quarter that of the larger cylinder.

Placing several metal objects inside the microwave, we see that sparks are created at the surfaces of these objects. These objects include steel wook, a fork, and a CD. 

The charge inside a conducting material is zero. All of the excess charge is location on the surface of the sphere.

Unlike a conducting sphere, whose charge lies entirely on the surface, an insulating sphere has charge that is allowed to move throughout the material. Both spheres have the same charge density. Solving for charge density therefore allows you to come up with an expression for an amount of charge inside a sphere of given radius. 

Enclosing a long thing conducting wire in a cylindrical gaussian surface will create a flux directed radialy outward, therefore the flux is due to curved part of the surface rather than the flat ends. Therefore, flux is equal to the electric field caused by the wire multiplied the area of the curved surface. 

The total electric flux through an enclosed surface equals the total charge enclosed in the surface divided by permittivity of free space ((8.854*10^(-12) * C^2)/(N * m^2)). This is equal the component of the electric field produced by the enclosed perpendicular to the surface multiplied by they area of the surface.